Github Linkedin Blog Projects

Bit hacking block boundaries

(Alliteration is awesome)

2025-07-24

Introduction

In Bedwars, not all blocks are breakable or interactable by the player, and not in all areas. Places such as the player's base and blocks already present in the map when the game started are not breakable, even if they are the coloured blocks which the player can buy from the shop.

This is also true for the reverse: There are many areas which players cannot place blocks either. This is usually the generators and the various bases of the players, and is also true for the powerups and tools they use: Popup towers, bridge eggs and tnt do NOT place over or destroy blocks in these restricted areas. This is further complicated by the fact that there are traps and areas of the map which can be enabled to benefit certain teams by giving them effects and notifying them of enemy presence, as well as boundaries for the map itself - if players go out of bounds, they are immediately eliminated. Teams also have personal blocks such as chests which only members of the same team can access, as well as a bed, which is a core block they must protect from different teams.

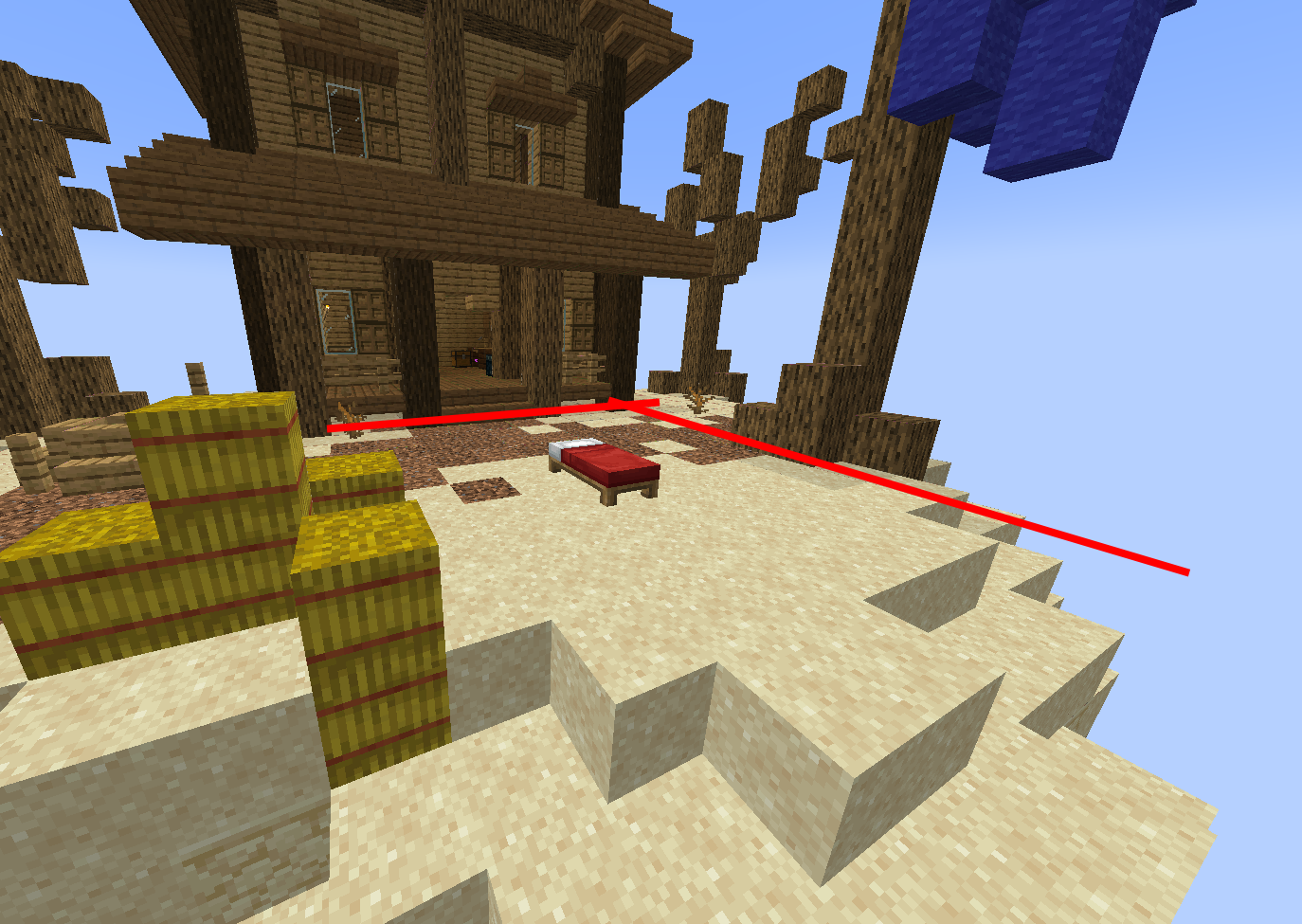
The average base of a team in a Bedwars match. The red lines demarcate a probable area which could be used as a boundary for where blocks can be interactable, and where they may be restricted.

Map by Weark on Stardix MC, obtained from PlanetMinecraft

The naive solution

In order to implement this functionality, one way we could achieve this is to track blocks by assigning them a tag. Consider we give each block a possible tag, consisting of a string, which determines the properties that the block has.

Spigot already has an API built for this which uses metadata stores. An idea is that for each block in the boundary of the arena, you could give the block some meta data, and then when an interaction happens, such as an attempt at a block break or place, you could either allow or cancel the event.

If we consider the naive solution, we can set a fixed metadata value for a block, which is plugin dependant. This allows multiple plugins to have metadata with the same label and not have conflict. What we would do is for every block in the 3-dimensional area, simply place a different string for different blocks for example "RED" for blocks which affect team red, and "RESTRICTED" for blocks which should not allow placement in the area.

The issue with this however, is that that we are working in a 3D area, which means for every block we scale the area up, the area scales cubically.


Imagine that we have a 200 x 50 x 200 arena area, which is a relatively small arena size. For simplification, lets imagine that we tag each block in the boundary, and the average size of the string that we use is 5 characters in length. In Java, a character in a string is 1 byte, so a string of length 5 is 5 bytes in size.

The order of growth of the memory required would be O(n^3) in this case, and although this isn't that significant of a memory overhead for this specific example, it is also important to consider how Spigot actually handles the creation of metadata.

When a block is assigned metadata, a few things happen. The metadata object is created, and then the metadata is actually assigned to the block.


The metadata which is created is a fixed metadata value, which inherits from lazy meta data. Because of the extra variables which are present in the superclass, setting a metadata value of 5 bytes may potentially result in much more memory used depending on factors such as the implementation of the callable object and soft reference.


This is further compounded by how the metadata is actually stored. In the block class, for each new label for the metadata, a new map is created to store that data. For the use of the minigame, this is entirely unnecessary and results in wasted memory.

Fixed metadata class


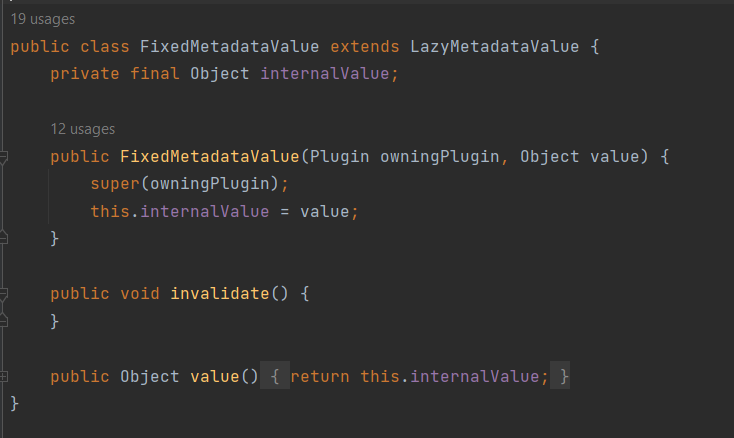
Lazy metadata class


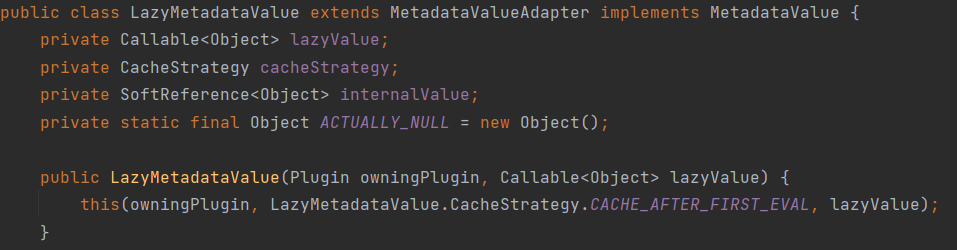
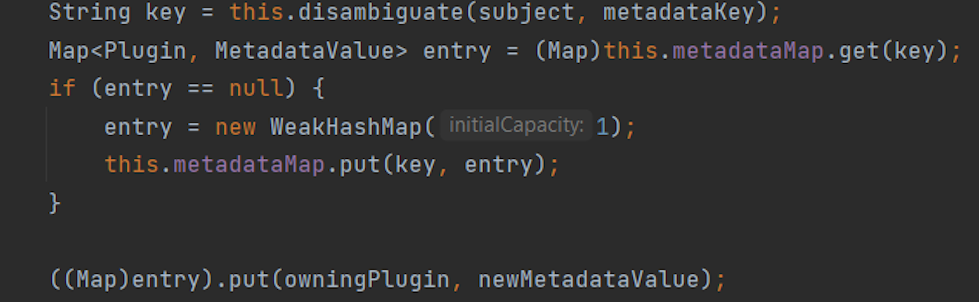
The metadata is validated and then set in the CraftBlock class

Fixes

If we choose to continue with this approach, one fix that we could use to bring down the memory, and potentially the CPU time to set the tags onto the blocks is to invert the selection of the arena and use bounding boxes instead for some boundaries.


Instead of tracking where the player can place blocks, we can instead track the blocks the player has placed instead, and assume all others are not breakable by the player. If the block has a tag that shows the player has placed it, then we can allow that block to also be broken when the player tries to break it as well. When the block has been broken, we would want to remove the tag from it so that it does not potentially interfere with other functions of the map.


Other boundaries, such as team effects and traps, can be implemented using bounding boxes which determine an area where they should be activated.

This method works decently for tracking blocks, but we can also do away with spigot's metadata system entirely to create solution customized to our particular use case.


Spigot acts as a translation between Minecraft's NMS (net.minecraft.server) server code, and a version independent API which developers use. Aside from meta data, there isn't much in the way of other decorators which could be used to track blocks.


Modifying the base block classes by defining a subclass would also be a horrible idea as it could cause issues with Minecraft's loading system, furthermore compounded by the fact that chunk reloads would remove any modifications placed onto the blocks.


Therefore a handler or external manager would be the preferable choice to managing block tags.

Hashing Introduction

In order for us to use a different tracking system for blocks, we must first determine how blocks should be tracked in the first place.


One way to do this is to use a hash function which relies on prime numbers to generate values for blocks using their coordinates. Another one would be to simply concatenate all of the coordinates into a string and use it as an id for the block.


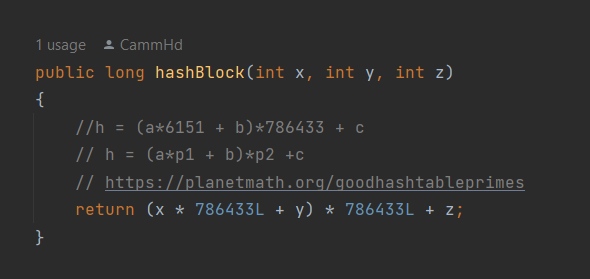
The issue with these 2 methods however is that the prime number method, although it performs decent for a good number of blocks, there is the chance that we will have a hash collision, which is significant as we may need to hash a large number of blocks, potentially in the millions. The issue with concatenation of coordinates is that if the coordinates are very large, say + or - 10 000 or more, then each id that is created will also be very large, resulting in increased memory use.

A better way to hash

Since the arena is a boundary defined by config, we can use these boundary coordinates to instead base our hashing function relative to these coordinates.


Because each block will potentially need an id, instead of generating large numbers from primes with the hope that they will be different from each other, we can instead simply, count all of the blocks from these relative coordinates. This will guarantee that each id is different and also allow us to use smaller numbers for storing these numbers, potentially allowing us to save more memory.


To do this, we will first translate the raw coordinates of the boundary of the arena to coordinates relative to the more negative of the two corners. Consider we have the raw coordinates c1 = (1,4,6) and c2 = (3,6,9).


Our relative coordinates would be r1 = (0,0,0) and r2 = (2,2,3). This is done by subtracting the difference of 0 to c1 from c2 and setting c1 to 0. To actually achieve the hash, we can think of our logic first in 2D and then in 3D.

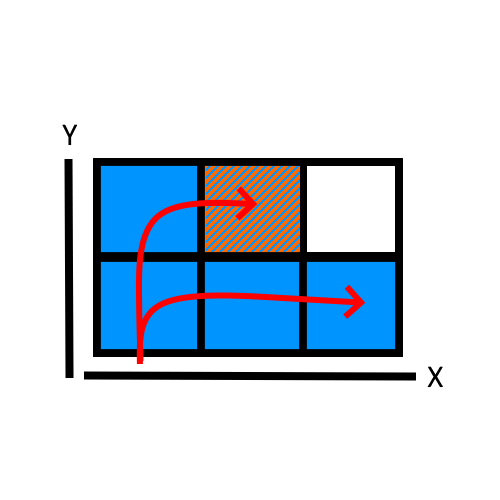
Consider a 2x3 grid as our boundary. If we want to hash the striped square, we will need to count the amount of completed rows which have come before it, and then know it's position relative to the closest row start. This is akin to grouping numbers in 10s and then calculating the remainder.


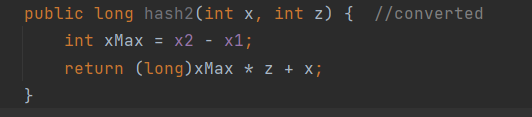
If we are counting relative to x, then this is the same as saying "count the completed rows on the x axis, and then add the remainder of the unfinished row". In this case, the striped block would be 1 completed row, and 2 extra, for which we can assign an id 5. If 0 indexed, would be 4. If the block's position is at the limit however, we have no remainder to add, and the id would be just x * y.


Below is the implementation code-wise but for the x-z plane.

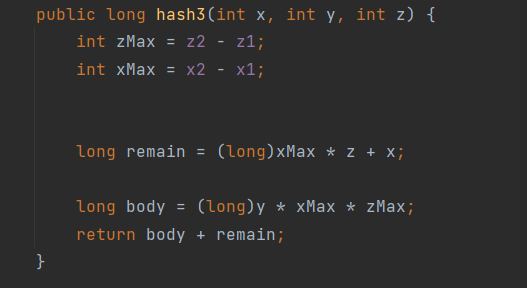
To expand this to the y axis, we can apply a similar idea. You can think of the solution for the x,z plane as the remainder of the grouping of 10s, which means that we need to calculate the groups next.

To calculate the full groups, we can simply take the y level of the block, and then multiply it by x and z lengths. Then we can add up the remainder and the groups to get the block id. This will allow all of the blocks in the boundary to be assigned a unique id. To take up the full range of possible numbers, we can also shift the numbers down to the minimum for the current data type and also convert the numbers to a different base.

Bithacking

In Bedwars, there are a maximum of 8 teams which can be in a given game at a time. This coincidently, is also the number of bits in a byte, which is a datatype in Java. What we can do then, is assign a bit in the byte to certain teams to allow us to tag certain blocks such as the team chests and beds as belonging to a certain team.


For example, team RED could have the byte representation of 1000 0000, and team BLUE could have the byte representation of 0100 0000. We can put each team into an array and assign them an index in the array so that they each have a bitwise representation. We also have 2 exceptional representations we can use as well: 0000 0000 and 1111 1111 which we can use to determine whether something is restricted in some way. To fully utilize this, we need to define bitwise operations and how we can place data onto bytes.


Sidenote: Obviously we could just instead take numbers and assign them to a team (E.g 1 -> team red, 2 -> team blue, etc), but that doesn't allow us to take advantage of using other possible representations which the bytes can take. Another thing to consider is that one of the main goals of this plugin was to learn, so an opportunity to utilize bit manipulation instead of switch/if statements was preferred at the time.

Writing data

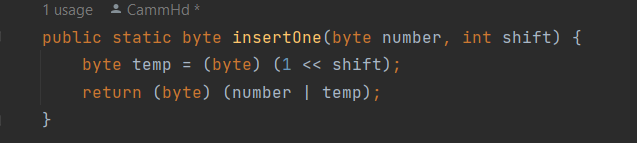
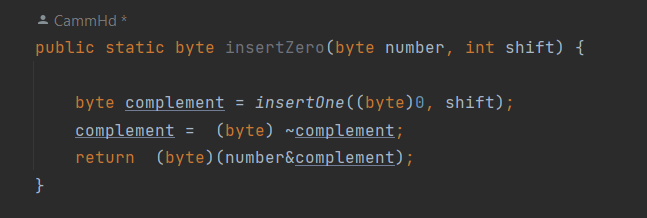
To write data, we need to insert 1s and 0s into certain positions of a byte without modifying the rest of the byte. To do this, we can create a dummy number which will have the 1 at the position we choose, and then bitwise OR that number onto our target number. By shifting to the right, it has the effect of multiplying the dummy number by 2^shift.

We can do something similar with deleting a 1 at a position. If we create a dummy number and then complement it, it will have a 0 at the position we will want to remove. If we then bitwise AND the number with our target, it will remove the 1 from the position in the target number.

Reading data

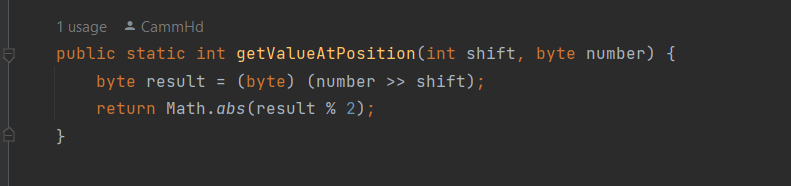
In order to read at a certain position, we can shift the byte until the bit we want to read is at the right most position. If we then divide this number and it has a 1 in that position, it will have a remainder not equal to 0. Otherwise, it will have no remainder.

Now instead of using a switch statement and continually checking each index to see whether there is a 1 in there to associate the tag with a team, we can do something interesting.

Logorithms

If you haven't noticed by now, whenever we take a shift of a number for a byte, we're really dealing with 2^n, where n is that shift. We can do the same to get information out of the number as well. Bytes by default are represented in 2s complement in Java, so in order to extract information we need to deal with a case where the byte is actually negative.


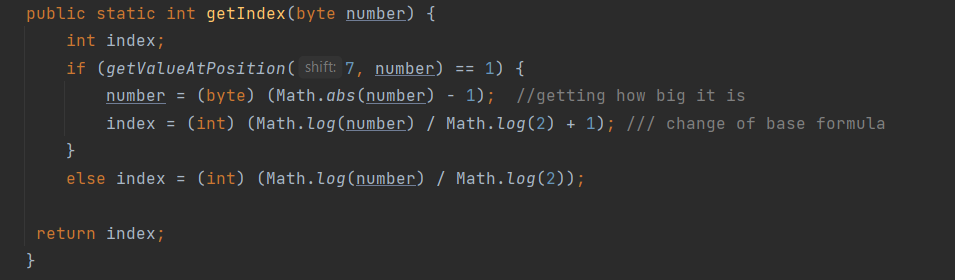
To get the index of the team, we can take the logarithm base 2 of the byte, but since Java only does log base 10, we need to use the change of base formula to change to base 2.


The index of the team is then defined by: index = log(byte) / log(2).


We also have a case where there is a 1 at the left most position of the byte. This automatically should mean that it refers to index 7. But let's make this interesting. If we have a byte such as 1000 0000 which is -128, if we absolute value it using Java's Math.abs(), it will give us an integer which we can then subtract 1 from. This gives us 127, which is the positive upper bound of a byte.


Since 2^7 is 128, when we log 127, it will give us a value of 6. Hence we add 1 to get the correct result. We can then immediately index an array using this value, giving us the team which this tag refers to, allowing us to finally store and track block boundaries effectively.